Gerrymandering as an approximation for cognitive biases
Sorry for the click bait title
In calculus — god what a terrible way to start off an article if you’re trying to retain readers; no turning back now — in calculus, we can approximate a function (such as a sine wave) by using a fancy thing called a Taylor series approximation. This allows us to use a much simpler function that is nice and cuddly wuddly with the original – and more importantly, we save on a lot of computing power.
By the same token, I would argue that gerrymandering serves as a “Taylor series approximation” for most cognitive distortions. Conveniently, gerrymandering deals with physical districts, so it provides us a clean visual of such distortions.
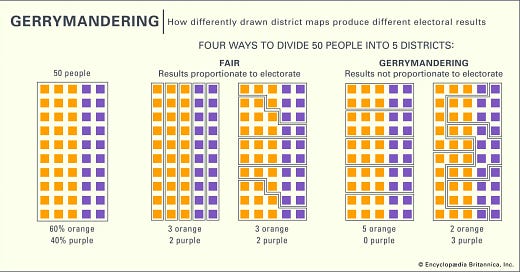
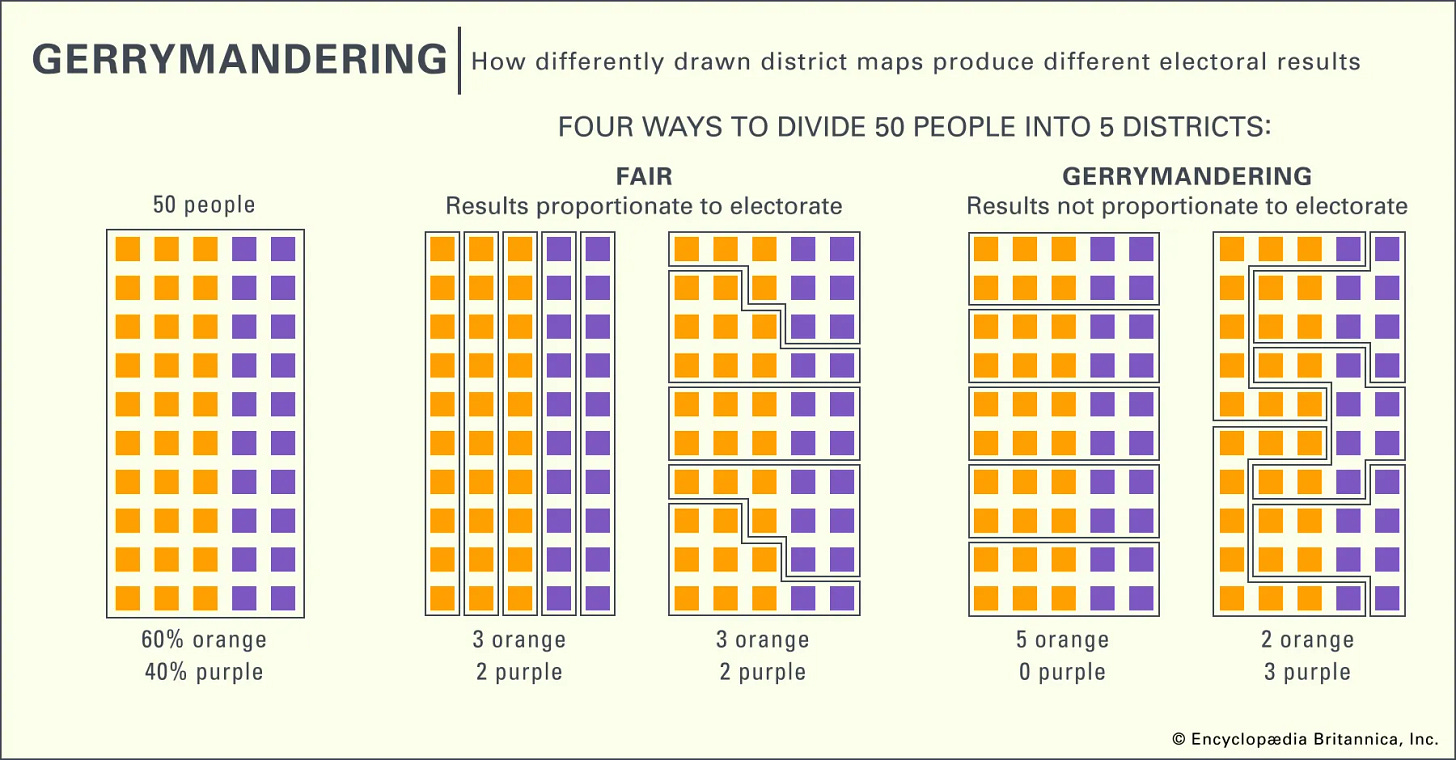
Taking the following image as an example:
In this case, the districts would represent the individual thoughts, beliefs, or ideas that a person may hold, and the colours would represent evidence in one direction or another.
Depending on how you define the parameter space, you might be getting all of the correct data in a narrow bandwidth, coming to reasonable independent conclusions — yet, overall, you would have a completely distorted idea of the broader picture.
It seems like a tedious point, but I would argue this shaping the fundamental architecture of the online information landscape; as more prominent writers have pointed out, people with agendas don’t even have to lie anymore. All they have to do is gerrymander their worldview.
Related reading:
Some examples of approximating distortions in this way:
Confirmation bias, hindsight bias, and the Texas sharpshooter fallacy are all versions of: “Let’s draw the boundaries afterward gathering the votes.” Creating the hypothesis after the evidence, so to speak.
Arguments from authority and ad hominem attacks are two sides of the same coin; “I completely (dis)trust these boundaries because XYZ person/group drew them.”
Learned helplessness, consistency bias, groupthink, the bystander effect, the just world fallacy, and arguments from ignorance are all different flavours of: “Well, I agree the boundaries aren’t great, but they must be there for a reason — so I’m not going to do anything about it.”
Whatever the distortion du jour, the underlying solution cannot stem from the confines of the given parameter space; rather, it’s necessary to redraw the boundary lines. Unfortunately, unlike Taylor series approximations, there’s no neat mathematical formula which allows us to do that in the real world.